Solving equations with variables on both sides is a fundamental algebra skill․ It involves simplifying expressions and combining like terms to isolate the variable․ These problems are essential for developing problem-solving strategies in mathematics, as they often appear in real-world scenarios and more complex equations․ Worksheets and practice exercises are widely available to help students master this concept, starting from basic problems to advanced challenges․ This section provides a comprehensive introduction to understanding and approaching such equations effectively․
1․1 Overview of the Concept
Solving equations with variables on both sides involves algebraic manipulation to isolate the variable․ These equations require simplifying expressions, combining like terms, and strategically applying operations to both sides․ Unlike equations with variables on one side, this concept demands careful handling of terms on both sides of the equal sign․ The goal is to find the value of the variable that makes the equation true․ This skill is foundational for higher-level math and real-world problem-solving, making it essential for students to master through practice and guided exercises․
1․2 Importance of Mastering This Skill
Mastering the skill of solving equations with variables on both sides is crucial for algebraic proficiency․ It enhances problem-solving abilities and analytical thinking, essential for advanced mathematics․ This skill is fundamental in various real-world applications, such as science, engineering, and finance․ By practicing with worksheets and exercises, students build a strong foundation for tackling more complex equations and word problems․ Understanding this concept instills confidence and prepares learners for higher-level mathematical challenges, making it a vital part of any algebra curriculum․
1․3 Structure of Equations with Variables on Both Sides
Equations with variables on both sides have expressions with variables and constants on each side of the equal sign․ These require simplifying and combining like terms to isolate the variable․ The structure involves strategic manipulation, such as distributing and moving terms to one side․ Recognizing this setup is key to applying effective solving strategies․ Visual methods, like algebra tiles, are often used to help students understand the balance needed to solve for the variable effectively in these structured equations․

Steps to Solve Equations with Variables on Both Sides
Simplify both sides, combine like terms, and isolate the variable by performing inverse operations to solve for its value effectively using algebraic principles․
2․1 Simplifying Both Sides of the Equation
Simplifying both sides of the equation is the first step in solving for the variable․ Start by performing any operations inside parentheses or applying distributive property to expand expressions․ Next, combine like terms on both sides to reduce complexity․ For example, in the equation 6r + 7 = 13 ⎯ 7r, simplify by combining constants on the right side․ This step ensures the equation is easier to work with before isolating the variable․ Always perform operations step-by-step to avoid errors and maintain balance in the equation․ Simplifying carefully sets the foundation for successfully solving the equation․
2․2 Combining Like Terms
Combining like terms is a crucial step in simplifying equations with variables on both sides․ Like terms are terms that have the same variable raised to the same power․ For example, in the equation 6r + 7 = 13 ⎯ 7r, the terms 6r and -7r are like terms․ Combine them by adding or subtracting their coefficients․ This process helps reduce the equation to its simplest form, making it easier to isolate the variable․ Always ensure that like terms on both sides of the equation are combined before proceeding to the next step․ This step is essential for maintaining balance and accuracy in the equation․
2․3 Isolating the Variable

Isolating the variable is the final step in solving equations with variables on both sides․ After simplifying and combining like terms, the goal is to have the variable alone on one side․ This is achieved by performing inverse operations to move constants and coefficients․ For example, in the equation 6r + 7 = 13 ⎯ 7r, adding 7r to both sides results in 13r + 7 = 13․ Subtracting 7 from both sides gives 13r = 6, and dividing both sides by 13 yields r = 6/13․ This method ensures the variable is isolated, providing a clear solution․

Example Problems and Solutions
Example 1: Solve 6r + 7 = 13 ⏤ 7r․ Combine like terms: 6r + 7r = 13 ⎯ 7, resulting in 13r = 6․ Thus, r = 6/13․
Example 2: Solve 13 + 4x = 1 + x․ Subtract x from both sides: 13 + 3x = 1․ Subtract 13: 3x = -12․ Thus, x = -4․
3․1 Solving 6r + 7 = 13 ⏤ 7r
To solve the equation (6r + 7 = 13 ⎯ 7r), start by getting all variable terms on one side․ Add (7r) to both sides:
(6r + 7r + 7 = 13), simplifying to (13r + 7 = 13)․ Next, subtract 7 from both sides:
(13r = 6)․ Finally, divide both sides by 13: (r = rac{6}{13})․ Verify by substituting (r = rac{6}{13}) back into the original equation to ensure both sides are equal, confirming the solution is correct․
3․2 Solving 13 + 4x = 1 + x
To solve (13 + 4x = 1 + x), first, subtract (x) from both sides to combine like terms: (13 + 3x = 1)․ Then, subtract 13 from both sides: (3x = -12)․ Finally, divide both sides by 3: (x = -4)․ Verify by substituting (x = -4) back into the original equation to confirm equality on both sides, ensuring the solution is accurate and complete․

Common Mistakes and Tips to Avoid Them
Common mistakes include mishandling negative signs and incorrectly combining like terms․ Always double-check operations and ensure equality is maintained․ Practice regularly to build accuracy and confidence․
4․1 Handling Negative Signs Properly
Handling negative signs properly is crucial when solving equations with variables on both sides․ Negatives can be tricky, as they affect the entire term they precede․ When moving terms, remember that subtracting a negative is equivalent to adding its positive counterpart․ For example, in the equation (6r + 7 = 13 ⏤ 7r), subtracting (7r) from both sides becomes (6r + 7r + 7 = 13)․ Always pay attention to the signs to avoid errors․ Highlighting or underlining negatives can help maintain clarity․ Double-checking work ensures accuracy and prevents mistakes from escalating․
4․2 Avoiding Errors in Combining Like Terms
Combining like terms accurately is essential when solving equations with variables on both sides․ Common errors include misaligning coefficients, forgetting to apply operations to all terms, or incorrectly combining constants and variables․ To avoid these mistakes, carefully identify and group like terms on each side of the equation․ Use highlighting or color-coding to distinguish between variable terms and constants․ Double-check each step to ensure operations are applied consistently․ For example, in the equation (6r + 7 = 13 ⎯ 7r), combining like terms involves adding 6r and 7r on one side and simplifying constants on the other․ Precision and patience are key to avoiding errors and ensuring correct solutions․

Practice Exercises
Practice exercises are essential for mastering equations with variables on both sides․ Worksheets range from basic to advanced problems, providing structured progression for skill development and confidence building․
5․1 Worksheet 1: Basic Problems
Worksheet 1 focuses on introductory problems designed to build foundational skills in solving equations with variables on both sides․ Problems like 6r + 7 = 13 ⎯ 7r and 13 + 4x = 1 + x introduce students to balancing equations and combining like terms․ These exercises emphasize clear steps: simplifying both sides, moving variables to one side, and solving for the variable․ The worksheet includes positive whole-number solutions, making it ideal for beginners․ By completing these problems, students develop confidence in handling basic algebraic manipulations and prepare for more complex challenges ahead․
5․2 Worksheet 2: Intermediate Problems
Worksheet 2 offers intermediate-level problems to enhance problem-solving skills․ It includes equations like -8p + 2p = -p ⏤ 3 and 4a ⏤ 4 = 8a + 12, which require applying previous skills․ Students practice combining like terms, handling negative signs, and isolating variables․ These problems introduce slightly more complexity, such as equations with negative coefficients or multiple steps․ Solving these reinforces algebraic principles and prepares students for advanced challenges․ The exercises are designed to build confidence and fluency in manipulating equations with variables on both sides, ensuring a solid understanding of the concept․
5․3 Worksheet 3: Advanced Problems
Worksheet 3 challenges students with advanced problems, such as equations involving fractions, decimals, or multiple variables․ Problems like 14 ⏤ 6b = 7 ⎯ 2b ⎯ 1 or 8 + x = x + 4 ⎯ 3x require meticulous step-by-step solving․ These exercises integrate concepts like handling negative signs, combining like terms, and isolating variables in complex scenarios․ They also introduce word problems, such as leaks in containers or hourly wages, to apply algebraic skills to real-world situations․ Solving these advanced problems strengthens algebraic manipulation and prepares students for higher-level mathematics․ Detailed steps and accurate calculations are crucial for success;
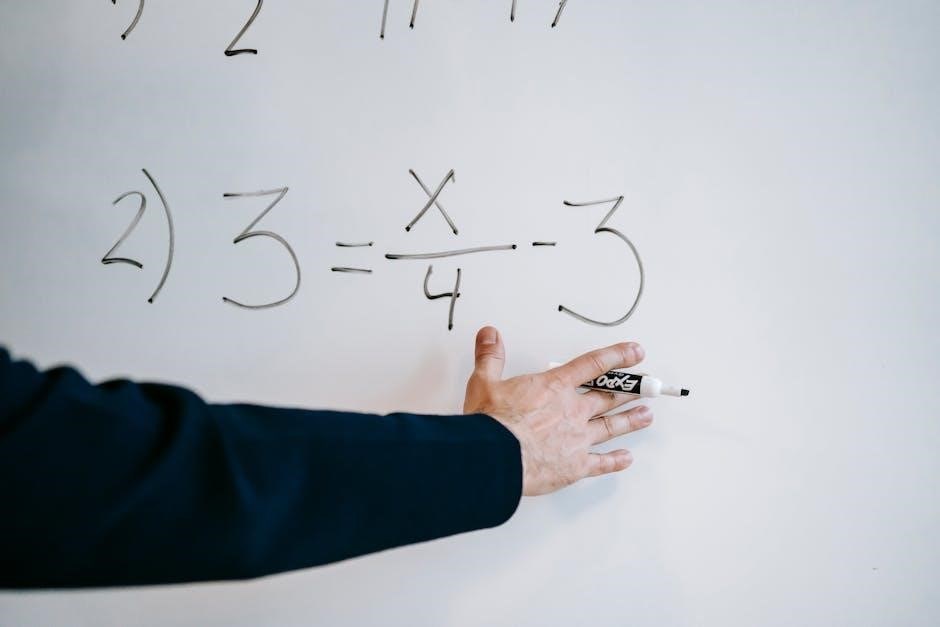
Word Problems Involving Variables on Both Sides
Word problems, like container leaks or part-time earnings, translate real-life scenarios into equations with variables on both sides․ These require forming algebraic equations and solving step-by-step to find unknowns, ensuring accurate algebraic manipulation and practical application of skills․
6․1 Translating Word Problems into Algebraic Equations
Translating word problems into algebraic equations involves identifying variables, constants, and operations described in the text․ For example, “Container A and Container B have leaks,” where their rates of leaking can be represented as variables․ Key steps include defining variables, interpreting phrases like “more than” or “less than” as addition or subtraction, and setting up equations that model the situation․ Practice exercises and worksheets help students master this skill, ensuring they can accurately convert real-world problems into solvable algebraic forms, fostering both mathematical and critical thinking abilities effectively․ This process is crucial for solving equations with variables on both sides, as it forms the foundation for applying algebraic techniques to find solutions․
6․2 Solving Word Problems Step-by-Step
Solving word problems with variables on both sides involves a systematic approach․ First, identify and define variables, then translate the problem into an algebraic equation․ Next, simplify both sides by combining like terms and isolating the variable․ For example, in problems involving leaks or part-time jobs, assign variables to unknowns like rates or allowances․Perform operations to gather variables on one side and constants on the other, ensuring equality is maintained․ Finally, solve for the variable and verify the solution by substituting it back into the original equation․ This methodical process enhances problem-solving skills and ensures accuracy in real-world applications․

Visual Methods for Solving Equations
Visual methods, like using algebra tiles, help represent variables and constants concretely․ These tools allow students to manipulate and balance equations, fostering a deeper understanding of algebraic concepts through hands-on learning․
7․1 Using Algebra Tiles
Algebra tiles are a hands-on tool for visualizing and solving equations․ Each tile represents a variable, constant, or operation, allowing students to manipulate and balance equations physically․ By arranging tiles on both sides of an equation, learners can see how variables and constants interact․ For example, adding or removing tiles from both sides helps maintain equality while isolating the variable․ This tactile approach simplifies complex algebraic concepts, making them more accessible, especially for visual and kinesthetic learners․ It also reinforces the idea of equality and the need to perform the same operation on both sides to solve for the variable․
7․2 Visual Representation of Variables and Constants
Visual representations, such as diagrams or charts, are effective tools for understanding equations with variables on both sides․ By illustrating variables and constants as distinct elements, these visuals help students grasp the balance required to maintain equality․ For example, variables can be represented as circles or blocks, while constants are shown as numbers or colored shapes․ This method allows learners to “see” the equation, making it easier to identify and move terms between sides․ Visualizing the problem also aids in isolating the variable, as students can track changes on both sides of the equation step-by-step․ This approach enhances comprehension and retention․

Teaching Strategies for Educators
Educators can employ structured lessons and interactive activities to effectively teach solving equations with variables on both sides, using algebra tiles and worksheets for reinforcement․
8;1 Structuring Lessons Effectively
Structuring lessons effectively for teaching equations with variables on both sides involves clear step-by-step instructions and hands-on activities․ Begin with an introduction to the concept, using real-life examples to illustrate its relevance․ Next, demonstrate the process of simplifying both sides, combining like terms, and isolating the variable․ Incorporate visual aids like algebra tiles or digital tools to enhance understanding․ Provide guided practice with basic problems before progressing to more complex scenarios․ Differentiate instruction by offering additional support for struggling students and challenging advanced learners․ Conclude with a review and homework assignment, such as PDF worksheets, to reinforce learning and allow for independent practice․
8․2 Engaging Activities for Students
Engaging activities for teaching equations with variables on both sides include hands-on tasks and interactive exercises․ Use algebra tiles to visually represent variables and constants, allowing students to manipulate and solve equations physically․ Incorporate group work, such as “Equation Solving Challenges,” where students compete to solve problems first․ Utilize real-world word problems to connect the concept to everyday scenarios, enhancing relevance and interest․ Technology integration, like educational apps or online simulations, can also captivate students and provide personalized practice․ These activities promote active learning and cater to diverse learning styles, ensuring students remain motivated and involved in the lesson․
Mastering equations with variables on both sides is crucial for algebraic proficiency․ Regular practice and real-world application solidify understanding and problem-solving skills․
9․1 Summary of Key Concepts
Solving equations with variables on both sides requires simplifying expressions, combining like terms, and isolating the variable․ Key strategies include moving variables to one side and constants to the other, ensuring balance by performing the same operations on both sides․ Mastery involves understanding how to handle negative signs, avoid errors in combining terms, and apply these skills to real-world problems․ Regular practice with worksheets and word problems reinforces these concepts, building confidence and proficiency in algebraic manipulation․ This skill is foundational for advanced mathematics and problem-solving․
9․2 Encouragement for Further Practice
Mastering equations with variables on both sides is a significant achievement, and consistent practice will further enhance your problem-solving skills․ Continue challenging yourself with worksheets and word problems to build confidence and speed․ The more you practice, the more intuitive these concepts will become․ Explore real-world applications to see how these skills apply in practical scenarios․ Regular review and application will solidify your understanding, preparing you for more complex mathematical challenges․ Keep practicing, and you’ll excel in algebra and beyond!